前言
本页面为矿大北京塑性力学神秘自编教材特供,正确性未知。
多看看黑色加粗的
—-某力土老师
意思是有名词解释,论述和计算题
第一章 绪论
1.1 关于塑性力学
塑性力学的基本假设
- 连续性假设
- 均匀性假设
- 在屈服前是各向同性
- 非粘性
- 稳定的或者递减强化的
- 塑性状态下不可压缩
- 弹性性质与塑性性质无关
1.2 关于塑性变形
初始屈服极限
在低碳钢拉伸实验中离开线性区域的应力称为屈服应力,作为塑性与弹性的分界点,称为初始屈服极限。
名义屈服极限
对于没有明显屈服阶段的材料,将卸载后残余应变为0.2%时所对应的应力作为屈服极限,称为名义屈服极限,用
\sigma_{0.2}表示
塑性/弹性/粘性变形
弹性变形在撤除外力后可以完全自行消除变形。
塑性变形撤除外力后无法消除部分变形。
粘性变形是由于时间增加逐渐消失的变形。
简单应力状态
施加的外力只产生一种基本变形,一般为单向拉伸,单向压缩以及纯剪切。
复杂应力状态
两种以上基本变形的材料内部应力状态叫做复杂应力状态
后继屈服点
连续加载屈服后释放荷载时的应力点称为后继屈服点
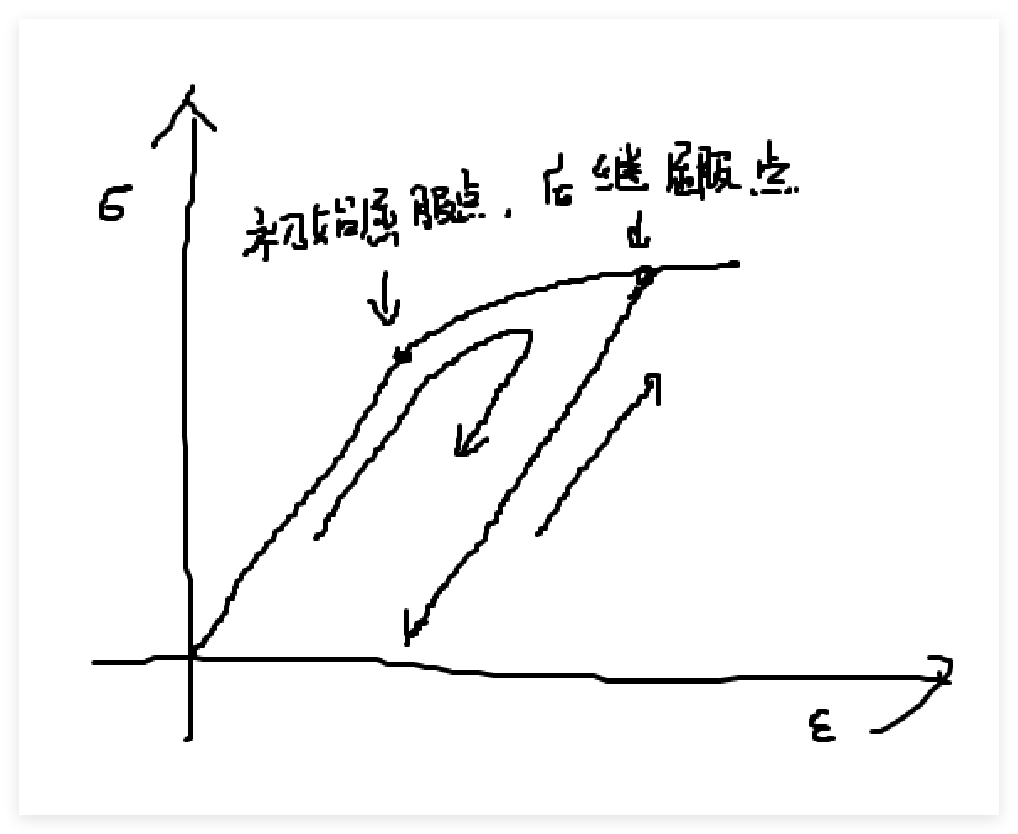
应变强化现象
卸载后再次加载,材料的屈服极限得到了提高,称为应变强化现象。
Bauschinger 效应
将材料拉伸至屈服,产生塑性应变强化后卸除载荷,再将其压缩(反向加载)至屈服,则压缩屈服极限明显小于拉伸屈服极限,这个效应被称作这一串字母效应。
影响
- 强化材料在一个方向提高屈服极限时,另一个方向的屈服极限降低。
- 初始各向同性的材料在发生塑性形变后变成各向异性。
静水压力
静水压力是均匀地施加在物体各个表面上的力,即各项均压。
一些结论:
- 静水压力不产生塑性变形,体积改变与压力大小为线性,纯弹性形变
- 静水压力下经书体积变化小,当成不可压缩。
- 与金属的初始屈服无关。
塑性变形的特点:
- 耗散形 不可恢复
- 应力应变关系并非一一对应,与加载路径有关
- 存在应变强化现象与Bau一串字母效应
- 静水压力不影响塑性变形,塑性状态下不可压缩。
几种材料
强化材料
后继屈服极限高于初始屈服极限的材料。
理想弹塑性材料
在外力下有明显的塑性流动阶段,流动阶段长,强化程度小。
理想钢塑性材料
弹性变形远小于塑性变形,不考虑强化与弹性变形。

稳定材料与不稳定材料
材料在应力增加时与应变增量为单调递增为稳定的,反之如果应力增量做负功,就是不稳定。
主要内容(?
初始屈服条件与后继屈服条件
在外力增加到一定程度时,材料内部某点由于应力打到极限而发生屈服,从这一点开始进入塑性变形阶段,这一点的应力状态称为初始屈服条件。
在达到初始屈服条件后卸载再重修加载,观察到的屈服应力高于初始屈服时,这种应力状态称为后继屈服状态。
本构关系
增量型本构关系与全量型本构关系
应力增量与应变增量一一对应,应变的大小取决于历史加载路径的应力应变关系称为增量型本构关系。
再简单加载条件下,在塑性状态下依然能够找到应变应力一一对应的关系的叫做全量型本构方程。
教材里面这一堆内容大概在第四章会开始讲
应力分析
一点的应力状态
应力矢量
物体内部一点的截面微元受力在截面面积趋于0的极限:
\mathbf{p} =\lim_{\Delta S \to 0} \frac{\Delta \mathbf{F} }{\Delta S} 方向取决于力的方向。
应力张量
我觉得不会考名词解释啊 但是这个处处都要用
[\sigma_{ij}]= \begin{bmatrix}
\sigma_x & \tau_{xy} & \tau_{xz}\\
\tau_{yx} & \sigma_y &\tau_{yz} \\
\tau_{zx} & \tau_{zy}&\sigma_z\end{bmatrix}三个正交的平面上必然有九个应力分量,其中由切应力互等定律可知切应力
\left\{\begin{matrix}
\tau_{xy}= \tau_{yx}\\\tau_{xz}= \tau_{zx}
\\\tau_{zy}= \tau_{yz}
\end{matrix}\right.体积应力
\begin{Bmatrix}
\sigma_{11} \\
\sigma_{22} \\
\sigma_{33} \\
\sigma_{12} \\
\sigma_{23} \\
\sigma_{31}
\end{Bmatrix}
=
\begin{bmatrix}
\lambda + 2\mu & \lambda & \lambda & 0 & 0 & 0 \\
\lambda & \lambda + 2\mu & \lambda & 0 & 0 & 0 \\
\lambda & \lambda & \lambda + 2\mu & 0 & 0 & 0 \\
0 & 0 & 0 & \mu & 0 & 0 \\
0 & 0 & 0 & 0 & \mu & 0 \\
0 & 0 & 0 & 0 & 0 & \mu
\end{bmatrix}
\begin{Bmatrix}
\varepsilon_{11} \\
\varepsilon_{22} \\
\varepsilon_{33} \\
2\varepsilon_{12} \\
2\varepsilon_{23} \\
2\varepsilon_{31}
\end{Bmatrix}广义胡克定律如上,或者换个人类点的写法就是
\begin{equation}
\begin{cases}
\varepsilon_{11} = \frac{1}{E} \left[ \sigma_{11} - \nu (\sigma_{22} + \sigma_{33}) \right] \\
\varepsilon_{22} = \frac{1}{E} \left[ \sigma_{22} - \nu (\sigma_{11} + \sigma_{33}) \right] \\
\varepsilon_{33} = \frac{1}{E} \left[ \sigma_{33} - \nu (\sigma_{11} + \sigma_{22}) \right] \\
\varepsilon_{12} = \frac{1}{2\mu} \sigma_{12} = \frac{1 + \nu}{E} \sigma_{12} \\
\varepsilon_{23} = \frac{1}{2\mu} \sigma_{23} = \frac{1 + \nu}{E} \sigma_{23} \\
\varepsilon_{31} = \frac{1}{2\mu} \sigma_{31} = \frac{1 + \nu}{E} \sigma_{31}
\end{cases}
\end{equation}把三个应变和应力表达式加在一起
\varepsilon_{x}+\varepsilon_y+\varepsilon_z = \Theta =\frac{1-2\mu}{E}(\sigma_x+\sigma_y+\sigma_z)=3k\thetaK=\frac{E}{1-2\mu}\theta其中应变之和为体积应变,后者为体积应力,K为体积模量,他们符合胡克定律。
平均应力,应力球张量与应力偏张量
“体积改变是弹性变形的一种体现,和塑性变形没有关系”
\sigma_m=\frac{1}{3}(\sigma_x+\sigma_y+\sigma_z)称为平均应力,则有对于一点应力状态的张量做运算
\begin{equation}
\bm{\sigma}^\text{sph} =
\begin{bmatrix}
\sigma_m & 0 & 0 \\
0 & \sigma_m & 0 \\
0 & 0 & \sigma_m
\end{bmatrix}, \quad
\bm{\sigma}^\text{dev} =
\begin{bmatrix}
\sigma_{11} - \sigma_m & \sigma_{12} & \sigma_{13} \\
\sigma_{21} & \sigma_{22} - \sigma_m & \sigma_{23} \\
\sigma_{31} & \sigma_{32} & \sigma_{33} - \sigma_m
\end{bmatrix}
\end{equation}前者为应力球张量代表应力的弹性部分,后者为应力偏张量,代表塑性部分。
\mathbf{S} =
\begin{bmatrix}
S_{xx} & S_{xy} & S_{xz} \\
S_{yx} & S_{yy} & S_{yz} \\
S_{zx} & S_{zy} & S_{zz}
\end{bmatrix}
=
\begin{bmatrix}
\sigma_{xx} - \sigma_m & \sigma_{xy} & \sigma_{xz} \\
\sigma_{yx} & \sigma_{yy} - \sigma_m & \sigma_{yz} \\
\sigma_{zx} & \sigma_{zy} & \sigma_{zz} - \sigma_m
\end{bmatrix}我们用S来表示这个偏张量,之后还大有用处。
应力不变量
主应力
在空间内任意一点的应力状态通过调整x,y,z轴方向,必然有一个是是的所有的切应力为0,此时的应力只有轴向应力,我们按照从小到大给他们叫做σ1,σ2,σ3。
要求解这个主应力,需要应力不变量。
应力不变量
物体内任意一点的主应力不会随着坐标系改变而改变,因此可以得到
\begin{align}
I_1 &= \sigma_{xx} + \sigma_{yy} + \sigma_{zz} = \sigma_1 + \sigma_2 + \sigma_3, \\
I_2 &= -(\sigma_{xx}\sigma_{yy} + \sigma_{yy}\sigma_{zz} + \sigma_{zz}\sigma_{xx} - \sigma_{xy}^2 - \sigma_{yz}^2 - \sigma_{zx}^2 )
=- \sigma_1\sigma_2 - \sigma_2\sigma_3 - \sigma_3\sigma_1\\
I_3 &= \det({\sigma}) = \sigma_1 \sigma_2 \sigma_3.=[\sigma_{ij}]= \begin{bmatrix}
\sigma_x & \tau_{xy} & \tau_{xz}\\
\tau_{yx} & \sigma_y &\tau_{yz} \\
\tau_{zx} & \tau_{zy}&\sigma_z\end{bmatrix}
\end{align} \begin{align} \sigma^3 - I_1 \sigma^2 + I_2 \sigma - I_3 = 0.\end{align}6式的三个解就是三个主应力。
应力偏量不变量
我们刚才求出的应力偏张量可以拿来耍一下了。
模仿上面应力不变量和主应力的定义:
应力偏张量的主应力为主偏应力,其不变量称为应力偏量不变量。
\begin{equation}
S_i = \sigma_i - \sigma_m, \quad \sigma_m = \frac{1}{3}(\sigma_1 + \sigma_2 + \sigma_3)
\end{equation}
\begin{align}
S_1 &= \frac{2}{3}\sigma_1 - \frac{1}{3}\sigma_2 - \frac{1}{3}\sigma_3, \\
S_2 &= -\frac{1}{3}\sigma_1 + \frac{2}{3}\sigma_2 - \frac{1}{3}\sigma_3, \\
S_3 &= -\frac{1}{3}\sigma_1 - \frac{1}{3}\sigma_2 + \frac{2}{3}\sigma_3.
\end{align}以上为主应力与应力偏张量的表达式
求解应力偏张量不变量的形式与应力不变量形式完全一致,懒得写了。
任意斜面上的应力
八面体
在主应力作为坐标轴的空间中,一个方向余弦的绝对值相同的平面,与任意坐标轴的夹角都相等,称为等倾面或者等斜面,这样八个平面合在一起叫做八面体,其上面每个平面的应力被记作八面体应力
\tau_{oct};\tau_{8}八面体应力
\begin{equation}
\sigma_\text{oct} = \frac{1}{3} (\sigma_1 + \sigma_2 + \sigma_3) = \sigma_m
\end{equation}\begin{equation}
\tau_\text{oct} = \frac{1}{3} \sqrt{(\sigma_1 - \sigma_2)^2 + (\sigma_2 - \sigma_3)^2 + (\sigma_3 - \sigma_1)^2} = \sqrt{\frac{2}{3} J_2}
\end{equation}\begin{equation}
\tau_\text{oct} = \frac{1}{3} \sqrt{
(\sigma_{xx} - \sigma_{yy})^2 + (\sigma_{yy} - \sigma_{zz})^2 + (\sigma_{zz} - \sigma_{xx})^2 +
6 (\sigma_{xy}^2 + \sigma_{yz}^2 + \sigma_{zx}^2)
}
\end{equation}顺便发现了八面体应力与主偏应力的表达式说是。
八面体应力在之后的屈服条件中极为有用,需要稍微记下来是怎么计算的。
应力强度
应力强度
以下式子就是应力强度,为了表征复杂应力状态下各应力分量的联合表征量,又叫做等效应力。
\sigma_i=\frac{3}{2}\tau_{oct}非常轻易的,结合(12)式,能够得到
\sigma_i=\sqrt{3J_2} 不难推导发现增加球应力不会影响应力强度,换言之,应力强度与应力球张量无关。
主应力空间
主应力空间,应力状态矢量与应力路径
以主应力取为三个互相垂直的直角坐标构成的空间直角坐标系,这个空间叫做主应力空间。
空间中的一点用矢量OP表示,叫做应力状态矢量。
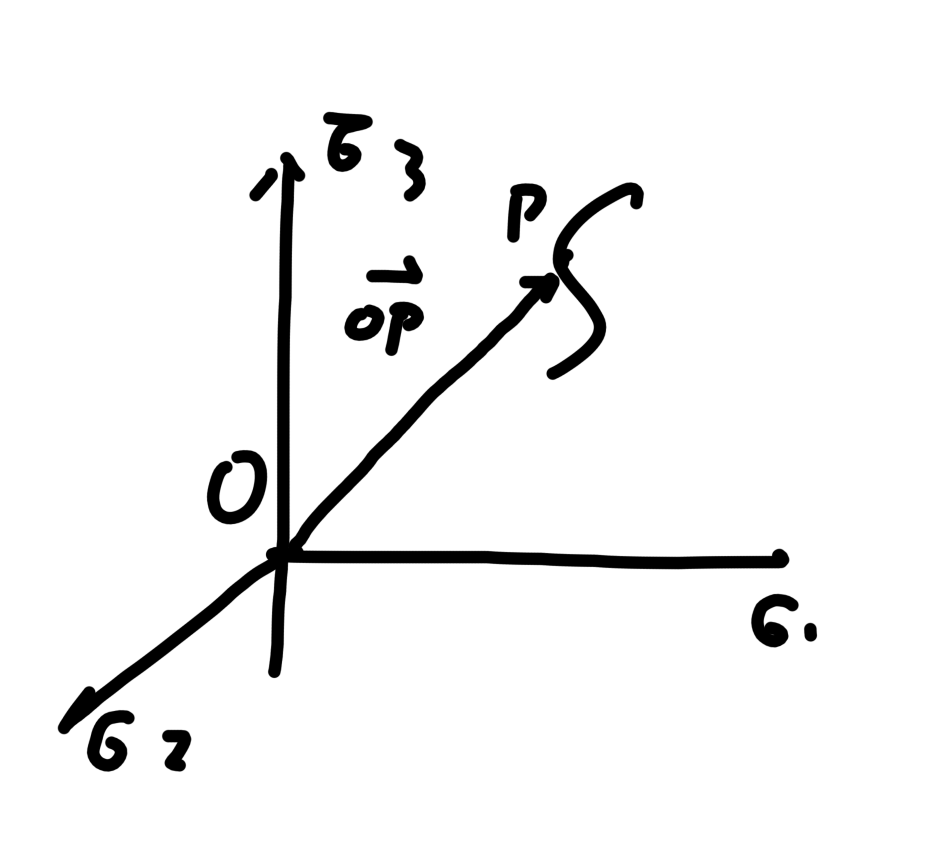
应力状态矢量在变化中的矢端描出的轨迹叫做应力路径。
等倾线与Π平面
在主应力空间内与三个坐标轴的夹角都相同的直线,称之为等倾线
垂直于等倾线且过原点的平面叫做Π平面
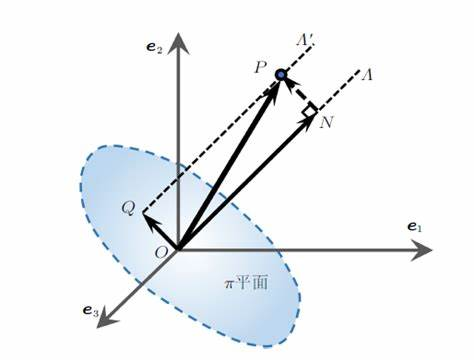
不难发现啊,L直线(等倾线)上的所有点应力偏张量全部为0,而Π平面则是球张量全部为0。
我们接下来的各类讨论全部在Π平面进行。
lode参数
首先我们把主应力往Π平面投影,并且把第二主应力对准y轴,向右为x轴
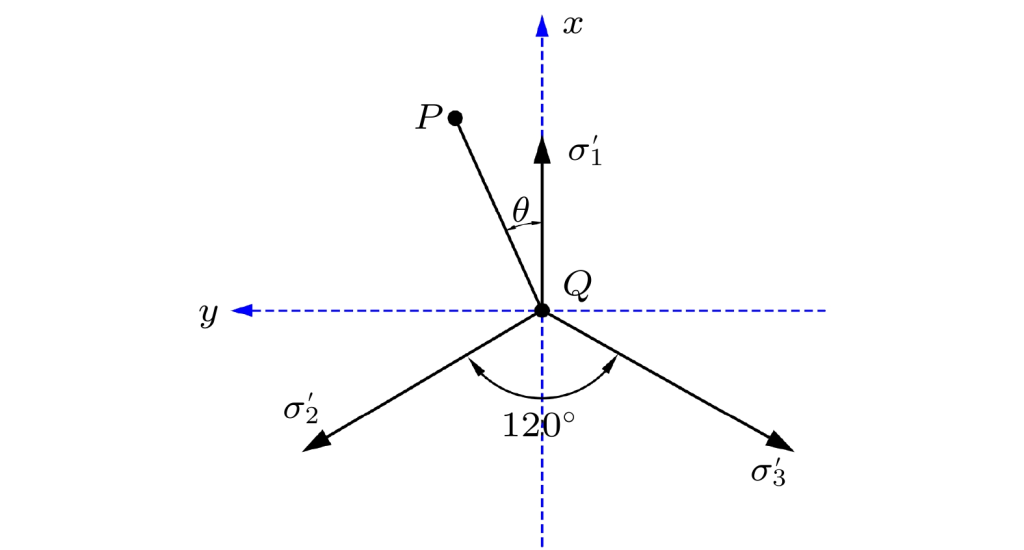
之后就能得到这三个主应力在Π平面的投影
我们把刚才的矢量OP投影上来的与x轴的夹角叫做lode应力角,同时定义lode应力参数和lode应力参数的应力偏量表达形式
\begin{equation}
\mu = \sqrt{3} \tan \theta = \frac{2\sigma_2 - \sigma_1 - \sigma_3}{\sigma_1 - \sigma_3}
\end{equation}\begin{equation}
\mu = -\frac{-S_1+2S_2-S_3}{S_1 -S_3}
\end{equation}应变偏张量,等效应变
我擦 这个和上面内容几乎一模一样,懒得写了。
需要注意的是
应变增量强度
\begin{equation}
\|\Delta \boldsymbol{\varepsilon}\| = \sqrt{\frac{2}{3} \, \Delta \varepsilon_{ij}' \, \Delta \varepsilon_{ij}'}
\end{equation}
上式就是应变增量强度的张量形式
然后是塑性应变增量强度,因为应变球张量为0,有意可以不考虑球张量。
\begin{equation}
\|\Delta \boldsymbol{\varepsilon}^p\| = \sqrt{ \frac{2}{3} \left[
(\Delta \varepsilon_{11}^{p'})^2 + (\Delta \varepsilon_{22}^{p'})^2 + (\Delta \varepsilon_{33}^{p'})^2 +
2 (\Delta \varepsilon_{12}^p)^2 + 2 (\Delta \varepsilon_{23}^p)^2 + 2 (\Delta \varepsilon_{13}^p)^2
\right]}
\end{equation}
lode应变参数
与主应力类似
\begin{equation}
\mu_\varepsilon = \frac{2e_2 - e_1 - e_3}{e_1 - e_3}
\end{equation}屈服条件
初始屈服条件
初始屈服条件
随着外力逐渐增加,物体内一点开始达到屈服极限时应力所满足的条件称之为初始屈服条件。
屈服面
在应力空间中,屈服条件是应力分量的函数,该函数在应力空间中对应的面叫做屈服面。屈服面在几何上是所有屈服点在应力空间的集合。
屈服曲线
屈服面与特殊平面的交线叫做屈服曲线,比如Π平面之类的。
屈服曲线与屈服面的四个性质
- 屈服面在主应力空间中平行于等倾面
- 屈服曲线是外凸的
- 在Π平面内屈服曲线关于三个主应力的投影直线堆成
- 同时关于他们的垂线也对称
其实第三条和第四条在说你只需要Π平面上1/12的曲线就能画完全部。
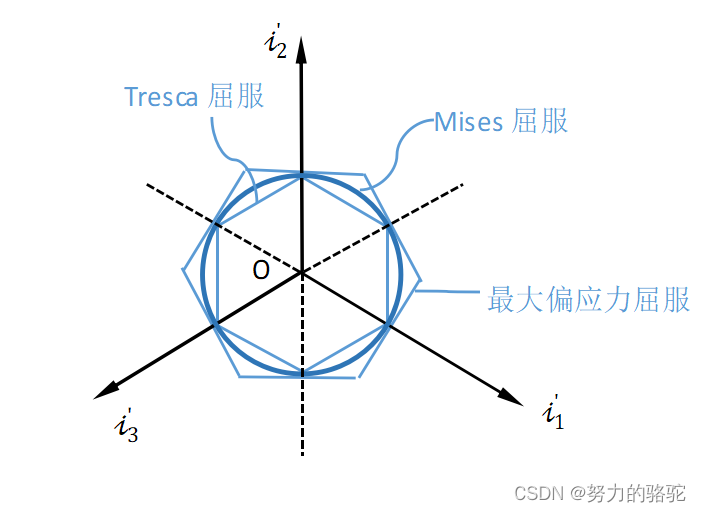
常用的屈服条件
tresca屈服条件
当材料的某一点最大切应力打到某个固有数值时,从该点发生屈服,这就是tresca屈服条件。
通常表达为
\tau_{max}=\frac{1}{2}k\sigma_1-\sigma_3=k=\sigma_{s}上文中的k其实是材料的拉伸屈服极限,是两倍的材料剪切屈服极限。
在平面应力状态下,可以表达为
\left\{\begin{matrix}
\left | \sigma _1-\sigma _2 \right | =k \\
\left | \sigma _2 \right |=k \\
\left | \sigma_3 \right |=k
\end{matrix}\right.
Mises屈服条件
当应力强度达到某一确定数值时,材料进入屈服,又称为应力强度不变条件。
与第二偏应力不变量满足以下关系
J_2=\frac{1}{3}k^2对于Mises屈服条件而言,k与剪切屈服极限满足
k^2 = 3 \tau_s^2
小插曲 薄壁条件下的应力状态分析
圆管的应力分析
懒得写
双剪屈服条件
当两个较大的主剪应力的绝对值之和达到某一数值时,开始屈服,叫做双剪屈服条件。
\begin{equation}
\begin{cases}
\tau_{13} + \tau_{12} = C & \text{当 } \tau_{12} \geq \tau_{23}, \\
\tau_{13} + \tau_{23} = C & \text{当 } \tau_{12} \leq \tau_{23}.
\end{cases}
\end{equation}
\\
\begin{equation}
\begin{cases}
\sigma_1 - \frac{1}{2}(\sigma_2 + \sigma_3) = \sigma_y & \text{当 } \sigma_2 \leq \frac{\sigma_1 + \sigma_3}{2}, \\
\frac{1}{2}(\sigma_1 + \sigma_2) - \sigma_3 = \sigma_y & \text{当 } \sigma_2 \geq \frac{\sigma_1 + \sigma_3}{2}.
\end{cases}
\end{equation}
后继屈服条件
后继屈服条件
在应力空间中后继屈服面也叫做加载面或强化面。后继屈服面在应力空间中可以用后继屈服函数或加载函数确定。
单一曲线假设
单一曲线假设认为,对于塑性变形中保持各向同性的材料,在各应力分量成比例增加的简单加载情况下,其强化特性可以用应力强度和应变强度的确定函数来表示
\sigma _i=\varphi (\epsilon _i)
适用于全量型本构理论,第四章会提到
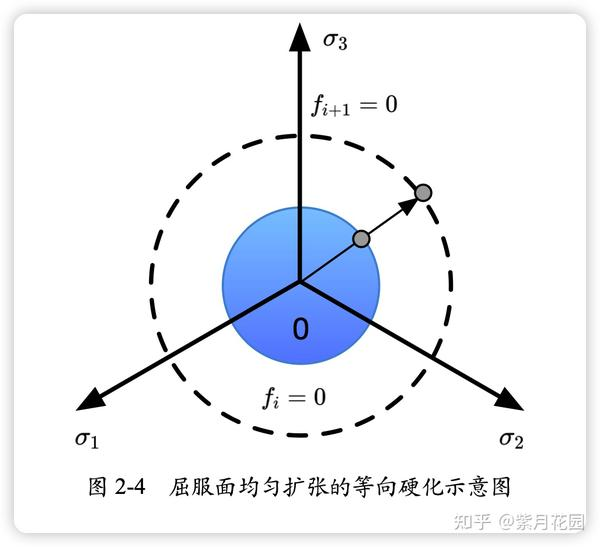
认为材料加载时在某一方向上强化,在相反方向会同样地强化。
随动强化理论
认为材料在某一方向上强化,就会在相反方向同等地软化。
加载和卸载准则
中性加载
应力点沿着屈服面变化,不产生新的塑性变形。
Drucker公设
塑性功
材料在塑性应变不能恢复的应变所散耗的能量叫做塑性功,其恒大于0。
Drucker公设
稳定材料塑性功不可逆的公设,称为Drucker公设,表达式为
\left\{\begin{matrix}
(\sigma _{ij}-\sigma _{ij}^0)\dot{}\mathrm{d}\epsilon _{ij}^p \geqslant 0 \\
\sigma _{ij}\dot{}\epsilon _{ij}^p\geqslant 0
\end{matrix}\right.Drucker公设的推论
- 屈服曲线的外凸性
- 塑性应变增量矢量与屈服面外法线方向一致(正交流动法则)
塑性本构关系
塑性本构关系的分类
全量理论
全量理论又称为形变理论,认为,在塑性状态下的应力与应变之间呈现全量关系。全量理论不考虑应力路径和加载历史的影响,直接建立了应力和应变全量方程。
增量理论
增量理论又称为流动理论,认为材料在塑性状态下的整个加载历史是由一系列微小增量组成的,应力和应变之间呈现增量关系。
广义Hooke定律
一般应力状态下,各向同性材料内部的应力和应变之间依然是线性关系,即为广义胡克定律。
\begin{equation}
\begin{cases}
\varepsilon_{11} = \frac{1}{E} \left[ \sigma_{11} - \nu (\sigma_{22} + \sigma_{33}) \right] \\
\varepsilon_{22} = \frac{1}{E} \left[ \sigma_{22} - \nu (\sigma_{11} + \sigma_{33}) \right] \\
\varepsilon_{33} = \frac{1}{E} \left[ \sigma_{33} - \nu (\sigma_{11} + \sigma_{22}) \right] \\
\varepsilon_{12} = \frac{1}{2\mu} \sigma_{12} = \frac{1 + \nu}{E} \sigma_{12} \\
\varepsilon_{23} = \frac{1}{2\mu} \sigma_{23} = \frac{1 + \nu}{E} \sigma_{23} \\
\varepsilon_{31} = \frac{1}{2\mu} \sigma_{31} = \frac{1 + \nu}{E} \sigma_{31}
\end{cases}
\end{equation}简单加载
简单加载也称比例加载,是指在加载过程中材料内任意一点的应力状态的各分量都按同一比例增加。
\sigma_{ij}=\alpha(t) \cdot\sigma_{ij}^0Ilyushin简单加载定律
满足以下四个条件的材料内部符合简单加载:
- 小变形,塑性变形小
- 外载荷成比例增加,载荷单调递增,位移边界条件必然是零位移边界条件
- 塑性状态下材料不可压缩,体积应变为0。
- 应力强度与应变强度为幂函数关系
\sigma_i=A\varepsilon_i^m
A与m都是常数
条件1,2为必要条件,3,4为充分不必要条件。
?
Hencky全量理论
\varepsilon_{ij}=\frac{1-2\mu}{E} \sigma _{ij}\delta_{ij}+\frac{1}{2G}S_{ij}+\lambda S_{ij} 应力与应变全量的关系如上
王宏伟说这里理论要后面来补充,那就等着吧。
Ilyushin全量理论
有以下基本假设
- 材料发生变形的体积变化是弹性的
- 应变偏张量和应力偏张量有相关关系
e_{ij}= \lambda\cdot S_{ij}于是其本构方程可以表示为
\left\{\begin{matrix}
\epsilon _ m =\frac{1-2\mu }{E} \sigma _m\\
e_{ij}=\frac{3\epsilon _i}{2\sigma _i}S_{ij} \\
\sigma_i= \varphi (\epsilon _i)
\end{matrix}\right.增量型塑性本构关系
Levy-Mises塑性流动法则(L-M流动法则)
LM法则更多的是对于理想钢塑性材料适用。
d\epsilon_{ij}= d\lambda\cdot S_{ij}应变增量与相应的应力偏量成比例。
Prandtl-Reuss流动法则(PR法则)
PR法则针对理想弹塑性材料。
d\epsilon_{ij}^p= d\lambda\cdot S_{ij}塑性应变增量与相应的应力偏量成比例。