前言
真的很难,这个真的很难。
你矿数学物理方法包含数学物理方程与复变函数两个部分,包难的。
复变函数
欧拉公式
通常来说复数应该表示为
w = u + vi
其中u与v分别是关于x与y的函数。
我们对于在复平面上的复数,用角度和模长来形容。
rsin\theta+rcos\theta i
通过泰勒展开不难发现上式之泰勒展开形式与下式泰勒展开形式一致
re^{i\pi\theta}遂得出欧拉公式
re^{i\pi\theta}=rsin\theta+rcos\theta i把左边想象成一个圆心在原点,角度控制的能转来转去的复平面上的箭头就可以,用这个能够解答很多问题
神秘小函数复变形式
一般这么考
i^i
这种题一般是把其看成某一个初等函数,然后把变量用复数形式表达
i^i = e ^{iln(i)}再把
i = e ^{i(\frac{\pi}{2}+2k\pi)}带入就能算出
e ^{-(\frac{\pi}{2}+2k\pi)}大体上题目都是这样,不是很难。
C-R条件,解析,可导
对于复变函数,输入与输出都是复数,要判断其可导必须用到偏导。
对于一个复变函数,满足下面偏导的式子就可以说明其解析。
g(z)=u+iv
\frac{\partial u}{\partial x}= \frac{\partial v}{\partial y}
;
\frac{\partial u}{\partial y}= -\frac{\partial v}{\partial x} 所以给出比如虚数部分你就能求出实数部分了。
计算留数
对于复变函数中不解析的点(其实就是分母为0了),可以计算他们的留数
要算留数首先要确定其阶数
f(z)=\frac{1}{(z-1)(z-2)^3}比如上面式子中z=1就是一个一阶的极点,z=2是一个高阶的极点
对于一阶的,计算非常简单
一阶极点计算留数
比如z0是一个极点,直接乘上极点的这一项,再取其极点值就行
Res_{z=z_0}f(z) =
\lim_{z \to z_0} (z-z_0)f(z)高阶极点计算留数
对于高阶,注意这里是(z-z_0)这个式子本身有幂次,而不是z有幂次
有以下之公式
Res_{z=z_0}f(z) = \frac{1}{(m-1!)}
\lim_{z \to z_0} \frac{d^m{-1}}{dz^{m-1}}(z-z_0)^mf(z)稍微算一下也能算出来,比如上面那个式子算出来应该是1
能计算留数就能继续算围道积分了
围道积分
直接使用留数定理
对于解析的区域,内部积分恒为0,所以需要考虑不解析的极点。
值得注意的是如果有不解析点在围道上,那就没法做
\oint_{C}^{} f(z)dz=2\pi i\sum Res(z,fz)用上面的办法把留数算出来加一块乘上2ipi就可以了
有的题目会比较几把不好算,有一个结论
函数的留数和为0,可以把好算的算出来推断,这个叫做留数定律,留数理论
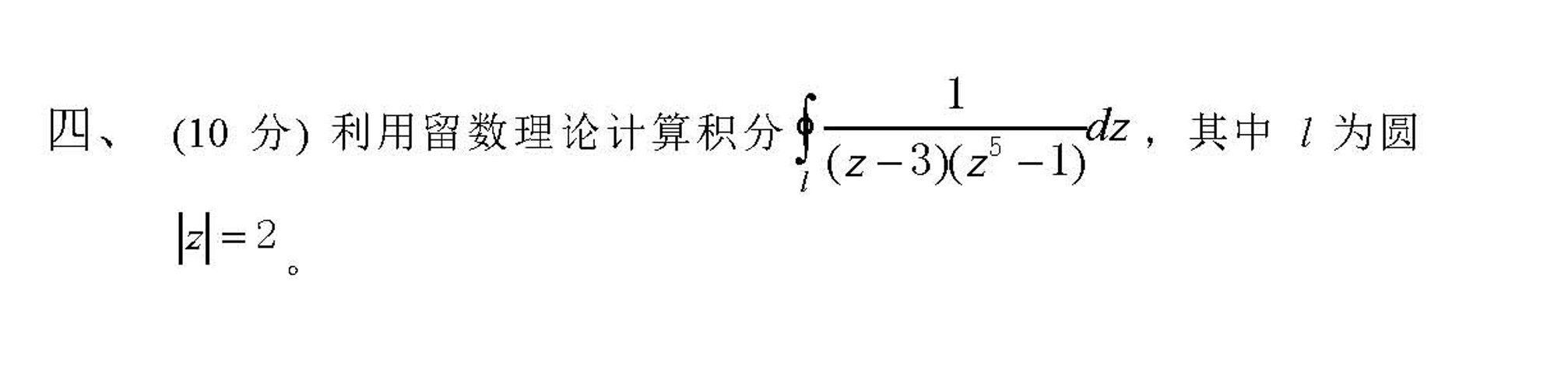
比如这个题,可以把z=3的留数算出来取反
级数展开,泰勒还是洛朗
洛朗展开是一个圆环,泰勒是一个圆,要求其内部全部为可解析的部分
题目给的解析中心如果是圆,那就没问题,直接泰勒画一个到最近不解析点的圆,这个圆到下一个不解析点的圆环用洛朗,最外面环到无穷也是洛朗展开
为了求得这个需要对中心点和展开方式分类
泰勒展开
对于一般内部解析的式子,用泰勒展开、
把需要求的式子拿来化为这个形式,或者拆成多个这种形式的合
\frac{1}{1-w}=\sum_{n=0}^{\infty}w^n ,\left | w \right | <1多个这个加在一起就是这个收敛半径内的泰勒展开
洛朗展开也大差不大,但是上面绝对值的部分肯定会出问题
洛朗展开
\frac{1}{1-w}=-\frac{1}{w}\cdot\sum_{n=0}^{\infty}\frac{1}{1-w^n },\left | w \right | >1注意留心拆分式就好了
求幂级数收敛半径

我擦 这不就是高数题,但是没关系其实也能做
仔细观察发现这个题给收敛拆分成了奇数项和偶数项,然后求各自的收敛半径,那肯定是不太行。
这种题不难发现奇数项与偶数项取极限的收敛值不一样,没法算
需要用根值判别
\sum_{k=0}^\infin a_k(z-z_0)^k的收敛半径R
R=\frac{1}{\lim \sup_{k\to\infin} \sqrt[k]{|a_k|} }这里的limsup是任何子序列中最大的一个子序列
带进去算
数学物理方程
三类基本数学物理方程
波动方程
u_{tt}=\frac{\partial^2 u}{\partial t^2} 热传导方程
u_t= D\bigtriangleup u+f
泊松方程
\bigtriangleup u=-h
给定狄拉克δ函数求积分
这个超级他妈简单
把后面的x,y,z值带进去就能算了
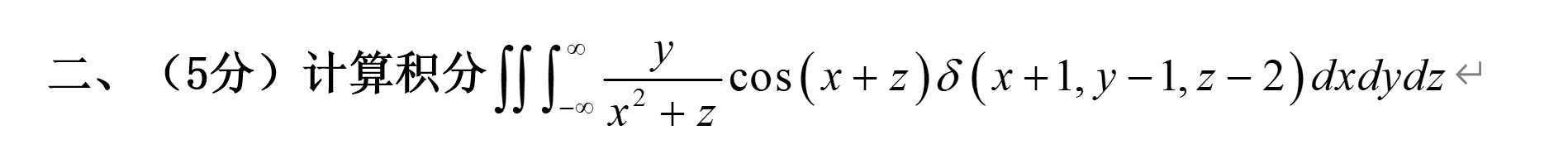
把x=-1,y=1,z=2带入前面函数即可
求泛函的变分
稍微有点点麻烦,但是也还好
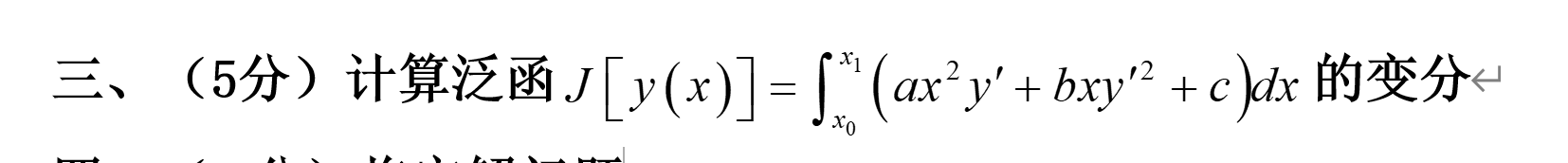
对于泛函的变分只用关注被积函数,设其为F
于是又泛函的变分等于
\delta J=\int_{x_0}^{x_1}(\frac{\partial F}{\partial y}\delta y +\frac{\partial F}{\partial y'}\delta y' ) dx所以只用把被积函数的偏导算出来 带进去,就可以下一步了
会分为有δy的和δy’的
前者不鸟他,后者需要进行分部积分把它算出来
对后者分部积分有巧思,因为函数的边界条件限制,可以取巧这样计算
直接把被积函数对于x求导,剩下直接抄δy’变成δy,变符号为负
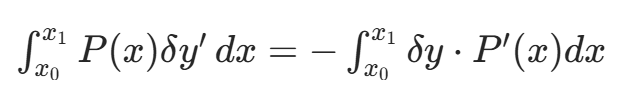
少问 多写。
泛函的极值
泛函的极值本质上是在做二阶常系数齐次线性微分方程
首先把第一个方程带入如下之公式
\frac{\partial F}{\partial y} -\frac{d}{dx} (\frac{\partial F}{\partial y'} )=0解的结果应该是一个二阶常系数齐次线性微分方程
之后就带入求特解就行。
如果给的方程含有y”的二次高阶导数,用这个
\frac{\partial F}{\partial y} -\frac{d}{dx} (\frac{\partial F}{\partial y'} )+\frac{d^2}{dx^2} (\frac{\partial F}{\partial y''} )=0化简会得到微分方程,该怎么解怎么解
如何分离变量
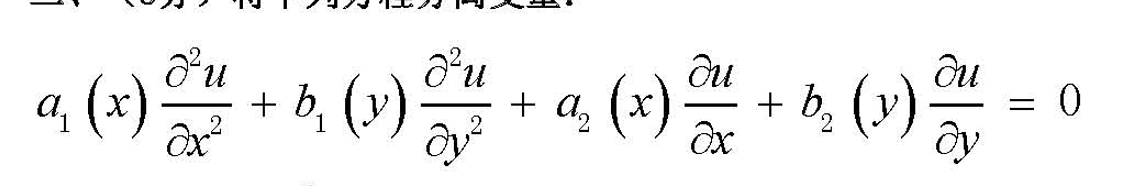
X(x)Y(y)=u(x,y)
要分离这个变量,就要按照题目给的算出需要的偏导数
\frac{\partial ^2u}{\partial x^2}=X''Y之后全部写出来把偏导数带入上面式子中
a_1X''Y+b_1Y''X+a_2X'Y+b_2X'X=0
直接代数计算就能分开两个式子,再统一令其等于一个常数,就能写出微分方程了
定解问题化为齐次边界条件
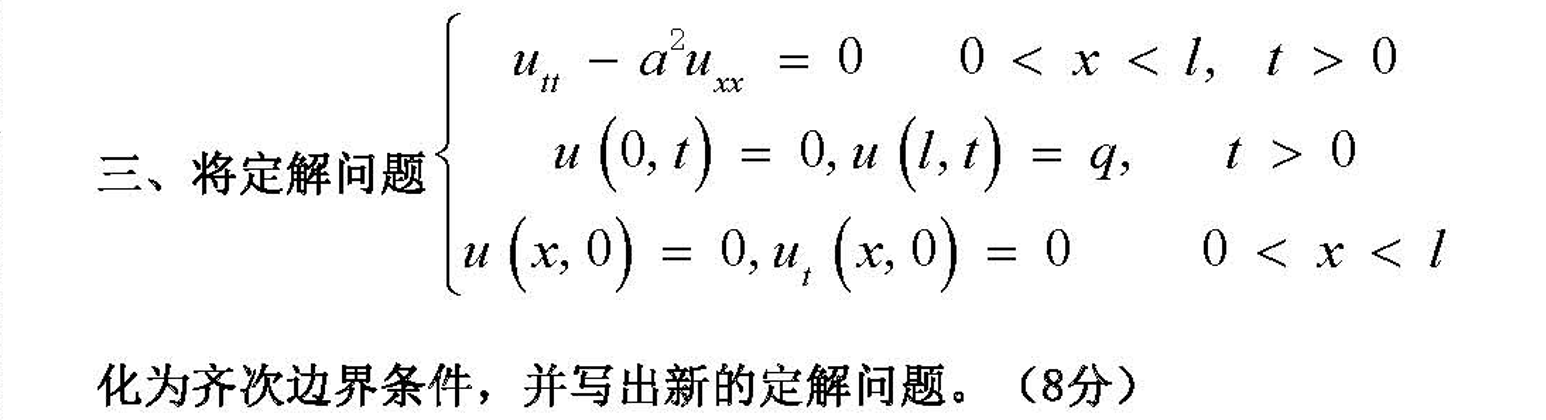
一般是这种题,需要构造辅助函数
u(x,t)=v(x,t)+w(x)
这个时候需要把w(x)设置为一个线性函数,来满足新的辅助函数边界条件齐次之要求
也就是
v(0,t) = 0; v(l,t)=0
原题中的二阶导数确保了
u_{tt}=v_{tt};u_{xx}=v_{xx}在装模做样对上面那式子通过求导证明后,就可以写出最后的齐次边界条件了
第一个式子和原始式子除了把u->v就没区别的
后面你需要自己算一下,也不麻烦
第二项应该是
u(0,t)=0;u(l,t)=0
第三项把
u = v +w
带入(w函数内的x保留)就能算出来
傅里叶变换与逆变换
对与一个函数要取其傅里叶变换形式,做以下变换
F(f(x)) = \int_{-\infty }^{\infty} f(x)e^{-i\omega t}dt有的时候会考这种

这种只用求-1,1区间的就行
算出来的东西还要写回积分表达式
f(x) =\frac{1}{2\pi} \int_{-\infty }^{\infty} F(x)e^{-i\omega t}d\omega不用算出来 写出来完事
